In my last article I discussed path finding using genetic algorithms. In that article I explained that we were using a path finding problem to have fun learning GA, but that in real life we'd want to use something far better suited to the problem, such as A*. Since most of the code was already written for the last article, I thought I'd owe it to you to give you an example of A* in action; and since any love story is really a path finding problem between two kindred spirits, why not do it on Valentine's Day?
Many of you may have learned about A* in school, as I did (back when dinosaurs roamed the Earth); it's a pretty simple algorithm used for finding the optimal path between two points, given an admissible heuristic. It is similar to a breadth-first search algorithm in that it will end up searching all of the nodes, so if a solution exists it will find it. To speed up the search, it uses heuristics so that only the most promising nodes are explored first.
The key components of A* are the following:
- HScore: Heuristic Cost - What is the estimated cost from the current node to the target?
- GScore: Movement Cost - What was the cost of getting to the current node?
- FScore: G + H
In our example, the heuristic cost will be the Manhattan Distance between the current node and the target node, which makes a lot of sense for us because our maze-walker from the last article is not capable of moving in diagonals. The movement cost will always be 1.
In English, the algorithm does the following:
- We select the node from the open list with the smallest F score. The open list is a set of candidate nodes (nodes that are traversable [e.g. not an obstacle] and that have not been walked yet). The first selected node is the starting node.
- We remove the current node from the open list and add it to the closed list. The closed list is a set of nodes that have already been walked.
- If the current node is the target node, we can return since the problem is now solved (yay!)
- Since we have not yet reached the target, we need to move from the current node. We'll look at the list of the current node's neighbors and
- If the neighbor is traversable and not in the closed list
- Calculate the G Score and recalculate the F score
- If the neighbor is not in the open list, we set it's parent to the current node add it to the open list
- If the neighbor is in the open list and has a smaller new F Score than what is stored currently, update the G and F scores in the node and set the parent to current
- Loop to the beginning. If the open list is empty then there is no path between start and target.
If you're interested in code, you can check out a c# implementation on GitHub.
So how much better is A* than our implementation using Genetic Algorithms? Here's a solution path using the same maze as the last article (now with a geeky Valentine's Day theme). It found the solution in milliseconds, whereas the GA took minutes!
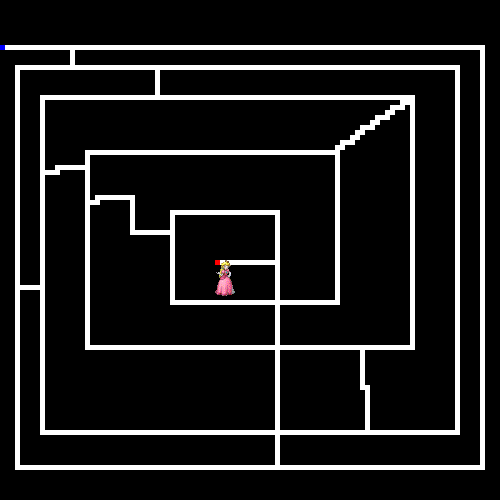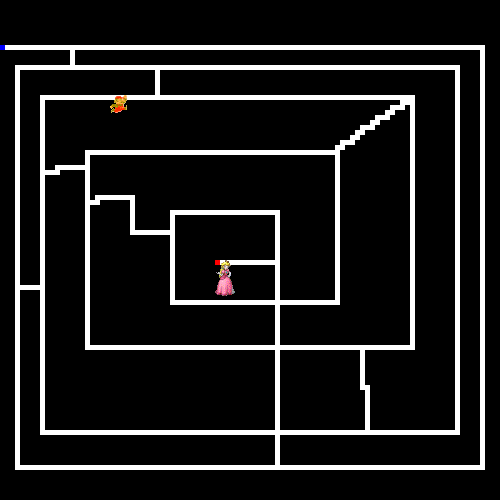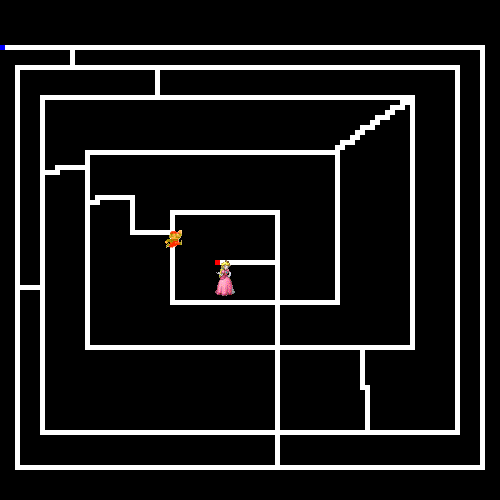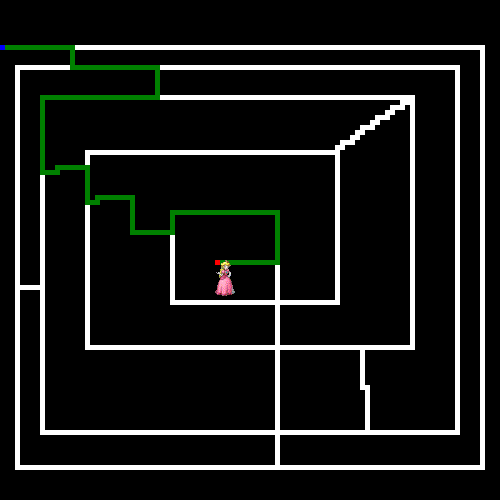
If you're interested in learning more about A*, with optimizations and tricks, check out this video series.
Happy coding and Happy Valentines Day!