I had read about genetic algorithms a long time ago, thinking to myself, "hey this sounds neat, I should try that one day!" Well, ten years later (what is that in Internet years?) I've finally scrounged up some time to play around with the concept. As with similar posts I've made in the past, I like to start off with a disclaimer: I've never formally studied genetic algorithms, nor do I claim to be an expert. I like to write about what I learn because it helps solidify the concepts in my head and because it forces me to actually finish small projects. Hopefully the reader learns something new, or corrects me where I get something wrong. In other words...

Code
The code for the project is available on Github.
The Problem Space
Before discussing genetic algorithms, let's briefly discuss the problem we will be throwing at it. Our little program will take in as input a maze (or if none is provided we will randomly generate one). Mazes are bitmap files, where the color black (#000000) is uncrossable and white (#ffffff) is a crossable path. A single blue pixel is the starting point and a single red pixel is the end point.
Here is an example (zoomed in) maze generated by the program.

The goal of the GA is to find the shortest path between the starting point and the end point.
Some notes if you're playing at home:
- We move one pixel at a time
- Our instruction set is "Up", "Left", "Down", and "Right." Note that we do not have the ability to move in a diagonal within a single step, so design your maze accordingly
As a final word before we get started, I want to just state that I selected this problem space because I thought it would be an easy project. There are other algorithms that are better suited to path finding, such as A*.
Genetic Algorithms
Genetic algorithms (GA) are adaptive heuristic searches based off of very (and I mean very) simple models of sexual reproduction and Darwin's theory of evolution. Like similar algorithms (hill climbing, simulated annealing, etc) GA's are a randomized search that use historical information to get closer and closer to the goal state. The GA difference is the use of crossover, where parts (genes) of a chromosome (algorithm) are spliced with another selected chromosome. Selection usually combines the best chromosomes together such that with each successive generation only the most fit chromosomes survive and reproduce. GA's also have a mutation component to them, where every so often some genes randomly mutate. This is to keep genetic diversity in the population and keeping us from getting stuck in local minima (or maxima).
Encoding
Chromosomes are made up of genes, and those genes need to be encoded. Binary encoding used to be the preferred method (as I will use), though other types of encoding can be used. Regardless, you'll need a way of reading a chromosome and interpreting the algorithm.
Example: Using a binary encoding, each gene will be two bits, and interpreted as follows:
| Gene |
Instruction |
| 00 |
Move Up |
| 01 |
Move Left |
| 10 |
Move Down |
| 11 |
Move Right |
An example chromosome would be 0100101100.
Population
A population is compromised of a set of chromosomes, from which some will be selected (discussed later) to reproduce into the next generation's population. You'd think that a very large population would introduce more variance into the population which would help yield better results, but bigger population sizes slow down the GA. Population sizes that I've seen recommended are 20-30, or 50-100, depending on the problem.
Crossover and Crossover Rate
As discussed earlier, crossover is the process of combining genes from one chromosome with genes from another. There are different crossover methodologies such as:
Single Point Crossover

Two Point Crossover

Uniform Crossover

(Above images taken from the Wikipedia article on GA crossover).
We will be using uniform crossover.
Not all chromosomes will crossover. The rate of crossover is determined by the crossover rate. The crossover rate is recommended to be high for best performance. We will be using 0.6, which is actually on the low end of recommendations.
Selection
Chromosomes from a population must be selected to mate to generate the next generation. There are few strategies, such as tournement or roulette wheel. Selecting the best chromosomes is called elitist selection. We will be using elitist selection.
Mutation and Mutation Rate
Randomly a GA will modify a chromosome's genes, based on the mutation rate. Unlike crossover rate, the mutation rate is suggested to be low. If the mutation rate is too high, it will be difficult to converge on good solutions because the GA will start diverging away. Some people like to start off with a higher rate to promote genetic diversity and slowly lower the rate through the generations to let evolution do it's work. There are multiple mutation strategies such as flipping a bit or swapping genes.
Fitness
Throughout this post we've been discussing "solutions," "best chromosomes," etc. But how do we know which chromosomes are the best? This is done via the fitness function, and this is really where all of the magic happens, and where you'll be spending most of your time experimenting. The meat and potatoes of our fitness function is shown below:
var steps = walker.Walk(out repeatedSteps, out closest);
if (steps < int.MaxValue)
{
steps = steps + repeatedSteps;
}
else
{
steps -= this.maze.Height * this.maze.Width * 50; // prevent overflow
var open = 0;
for (int x = 0; x < this.maze.Width; x++)
{
for (int y = 0; y < this.maze.Height; y++)
{
if (m[x, y] == Maze.State.Open)
{
open++;
}
}
}
steps += (open * 50) + ((int)closest * 2);
}
return -(steps);
The Walk() method (not shown) walks the genes of the chromosome, where each gene represents an instruction for a step to be taken in the maze. Walk() counts the total number of steps taken. Steps that were crossed one or more times are represented by repeatedSteps. A repeated step is weighted by the number of repeats. For instance, if the number of steps taken were 10, and 2 pixels were repeated 5 times, repeatedSteps would be 5, not 2. If Walk() does not encounter End, steps returned will be Int.Max. If End is encountered, instructions past End (in terms of genes in a chromosome) will not be counted as steps. Walk() will also return the closest point to End encountered in the walk.
If the walk reaches the end point, we return the negative of steps, since the goal is to minimize the number of steps taken (so fitness is highest when the score is lowest). To discourage the algorithm from walking around like a drunken sailor, we add repeatedSteps to steps (to give a lower fitness).

What do we do when the walk has not encountered the end point? Here we get a little creative to help (we hope) the GA converge faster. In this situation, we sort of want the opposite of what we wanted earlier; we want to encourage more steps so that we cover more ground in search of the end point. We also give a slight preference to chromosomes that edge toward the endpoint.
Performance
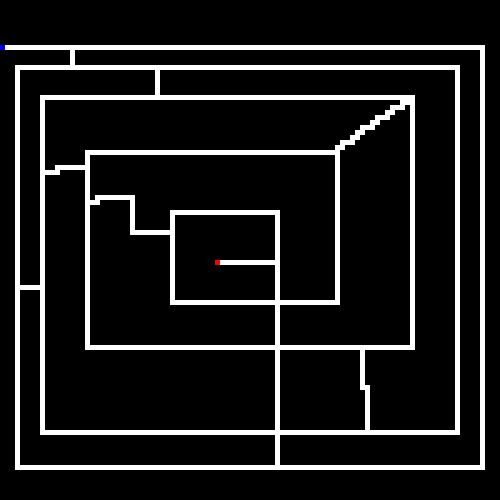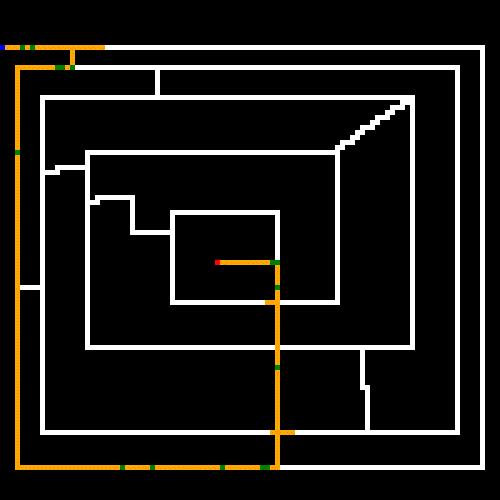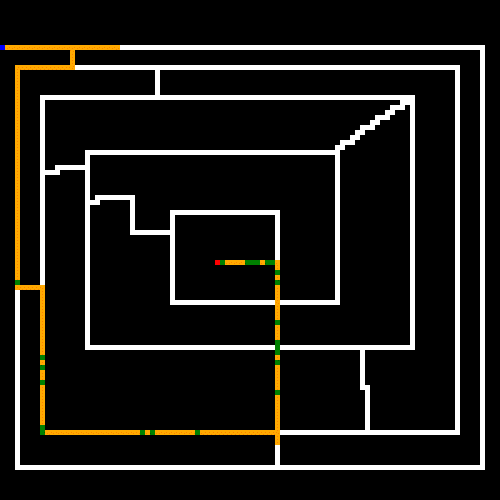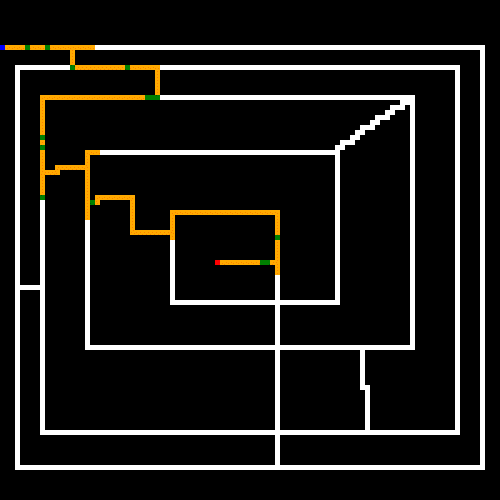
So how does our GA perform? Here's a run on a randomly generated maze. It was instructed to stop at 5 minutes or at stagnation, which was set at 300 (meaning no new better was found within 300 generations).
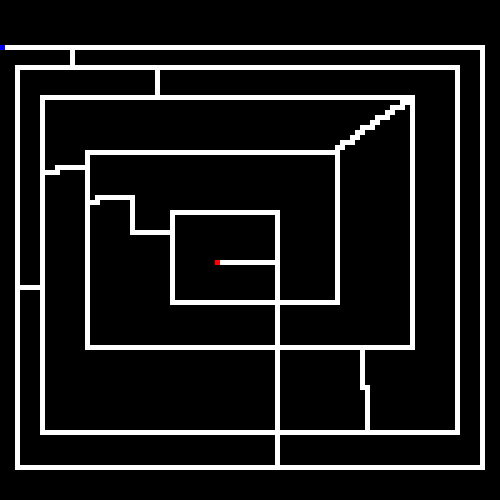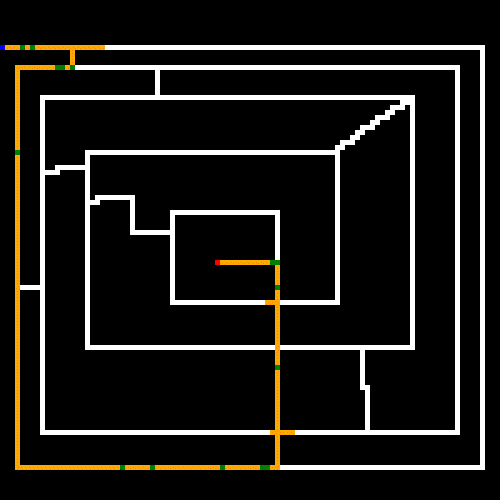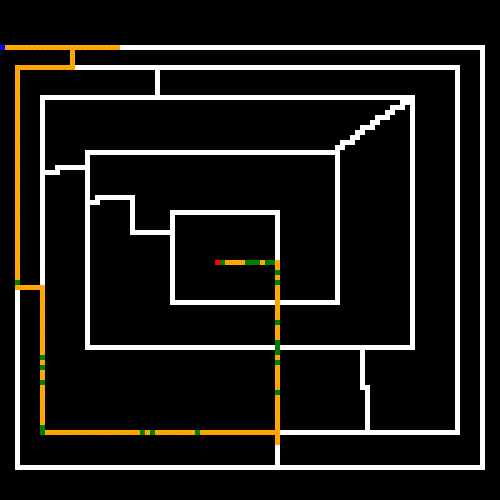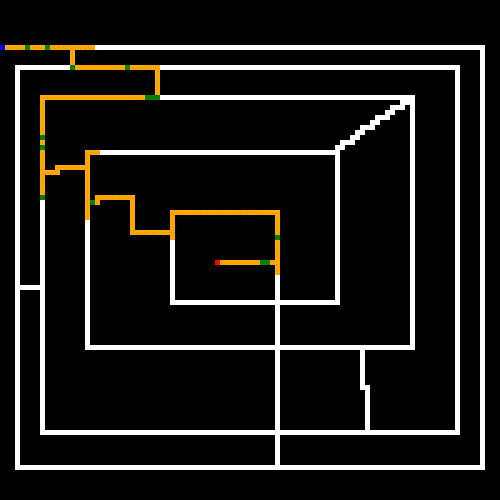
As noted earlier, the white lines represent the crossable paths, the blue point is the where we start and the red point is the target. Green represents paths that were only crossed once, and yellow are steps that repeated one or more times. We can see that the algorithm quickly found the shortest path and then optimized away most of the repeated steps. Setting the stagnation rate to a higher number would have optimized the remaining repeated steps away.
Now let's try a maze that I hand crafted. In this case the GA was still finding better and better results before we hit the 5 minute cap (by the way, all of these caps are configurable via command line options, but 5 minutes was the extent of my patience. Use the --help switch for a list of options). It looks like here the GA was close to finding the shortest path, but still had much optimizing to do to get rid of the repeated steps.
Finally, can we come up with a maze that tortures our GA? Here's what I came up with. While this is laughably easy for a human, it kills our GA because it will take a boat load of mutations before it covers the entire maze to find the end point (note that the start and end are on the opposite ends of the maze, and there is only a single path). I set the parameters to (what I thought) were obscenely large numbers. Apparently not obscene enough though; this run terminated at the 50 minute mark without ever hitting it's goal; though you can see that it got close and would have hit it's goal sooner than later. I wouldn't want this thing driving my taxi around town though.

Libraries Used
GeneticSharp is a genetic algorithm library that's pretty easy to use and has a bunch of options and is well documented and is actively maintained. As I've stated earlier, I'm far from an expert in GAs, so I can't speak to the quality of the library when compared to others, but given all of the positive aspects I noted I imagine that it is a strong contender.
Command Line Parser is a library for parsing command line arguments. I almost feel silly for saying this, but I'd never considered even looking for a library for parsing command line arguments and for displaying help hints; leading me to reinvent the wheel quite a few times (and probably a poor job in doing so). This library can be a fantastic addition to any console application.
Gifed is a library used for making animated gifs. Finding a gif library was more challenging than I thought it would be, and finding an easy to use library was even harder. This one did a great job though.
Notes
Every so often the program would throw an error that I had never seen before; "Attempted to read or write from corrupted memory." Very odd, I certainly am not using any unmanaged code (I'm not sure where in managed code memory would get corrupted), and I briefly looked through GeneticSharp and didn't see any unmanaged code in there either. Perhaps the issue is further down the stack, such as in his use of the SnippetSmartThreadPool library. It was quite annoying to have a long running evolution get stopped by an exception, so my solution was to catch the exception and not evaluate the "corrupted" chromosomes. Note that this type of exception cannot be caught normally, so I had to use [HandleProcessCorruptedStateExceptions].
Final Thoughts
While I had fun with the project, should I now use GA's anywhere I need a heuristic search (not that I personally run into that need often)? No, I don't think so. The entire time I was working on this project, it just felt like a good fitness function with some randomness would yield similar results. Apparently I am not alone in this. As I later looked for sources to write this post, I ran into the following:
and then the following quotes:
[I]t is quite unnatural to model applications in terms of genetic operators like mutation and crossover on bit strings. The pseudobiology adds another level of complexity between you and your problem. Second, genetic algorithms take a very long time on nontrivial problems. [...] [T]he analogy with evolution—where significant progress require [sic] millions of years—can be quite appropriate.
[...]
I have never encountered any problem where genetic algorithms seemed to me the right way to attack it. Further, I have never seen any computational results reported using genetic algorithms that have favorably impressed me. Stick to simulated annealing for your heuristic search voodoo needs.
— Steven Skiena
That's not to say that GA's have never been used to produce anything. Here's an antenna used by NASA that was "designed" by a GA (Source):

I'd love what some of you that have more experience with this type of thing have to say about it!
Follow Up
In response to this post, a Redditor made the following comment, which I thought was fantastic:
Every time an article pops up about GA, I'm excited again for the prospect of finding something useful to do with GA. And every time I'm disappointed again.
While I commend the author for implementing a genetic algorithm for path finding, what the author does is really just evaluating random walks and selecting the best. Sure, there is a bit of breeding in there, but especially the last example shows that we're basically waiting for a random walk to the end of the tunnel, and then would use GA to "optimize" away the unnecessary steps. In fact, this could be more easily achieved by preprocessing the labyrinth and turning it into a graph of possible routes. All the shown examples would have been solved much quicker had the GA algorithm not tried to step its way through it.
At least, the GA algorithm should have killed solutions that back-track, ie. that cross their previous path, immediately, since those solutions are never good solutions. This would have turned it into somewhat of a genetic Dijkstra.And at the very least, the GA algorithm should have dis-allowed immediate backtracking, ie. taking a step and then stepping back, which would have helped with the last labyrinth massively and with the others greatly.And that's the main gripe I have with GA in general: you implement something silly and random and get very bad solutions that take ages. Then you add a bit of domain knowledge, then a bit more and another bit more until you finally arrive at a regular algorithm for solving your problem. If you go that far before you give up.
Note that any of the well-known path-finding algorithms would have solved each of these mazes in milliseconds.
...
Here's another point I'd like to make in connection to what the guy said: GA isn't an optimization algorithm, it's a search algorithm. It searches really well if your solution space is full of viable solutions, without any obvious gradients and very rich in non-obvious parameters. The kind of problems we usually apply it to (like path-finding or crossing-minimization or any of the well-defined NP problems) aren't like that, and that's why we see no real benefits with GA over them.
And if you look at the inspiration for GAs, biological systems, that's exactly how they are: lots of parameters with rather un-defined functions (genes), lots of solutions (basically any combination of millions of genes) and completely non-obvious gradients.
Also bonus points for being greatly parallelizable, because that's another real benefit if you're doing massive searches.
- habeamus
Regarding his/her note about GA's and path-finding; I did find it necessary to point out at the beginning of my post that an algorithm like A* would be far better at pathfinding than a GA. I really hope that this isn't lost on anyone reading.